Set theory
| Part of a series on | ||
| Mathematics | ||
|---|---|---|
|
|
||
|
| ||
Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathematics – is mostly concerned with those that are relevant to mathematics as a whole.
The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of naive set theory. After the discovery of paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox), various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied.
Set theory is commonly employed as a foundational system for the whole of mathematics, particularly in the form of Zermelo–Fraenkel set theory with the axiom of choice. Besides its foundational role, set theory also provides the framework to develop a mathematical theory of infinity, and has various applications in computer science (such as in the theory of relational algebra), philosophy, formal semantics, and evolutionary dynamics. Its foundational appeal, together with its paradoxes, and its implications for the concept of infinity and its multiple applications have made set theory an area of major interest for logicians and philosophers of mathematics. Contemporary research into set theory covers a vast array of topics, ranging from the structure of the real number line to the study of the consistency of large cardinals.
History
[edit]Early history
[edit]
The basic notion of grouping objects has existed since at least the emergence of numbers, and the notion of treating sets as their own objects has existed since at least the Tree of Porphyry, 3rd-century AD. The simplicity and ubiquity of sets makes it hard to determine the origin of sets as now used in mathematics, however, Bernard Bolzano's Paradoxes of the Infinite (Paradoxien des Unendlichen, 1851) is generally considered the first rigorous introduction of sets to mathematics. In his work, he (among other things) expanded on Galileo's paradox, and introduced one-to-one correspondence of infinite sets, for example between the intervals and by the relation . However, he resisted saying these sets were equinumerous, and his work is generally considered to have been uninfluential in mathematics of his time.[1][2]
Before mathematical set theory, basic concepts of infinity were considered to be solidly in the domain of philosophy (see: Infinity (philosophy) and Infinity § History). Since the 5th century BC, beginning with Greek philosopher Zeno of Elea in the West (and early Indian mathematicians in the East, mathematicians had struggled with the concept of infinity. With the development of calculus in the late 17th century, philosophers began to generally distinguish between actual and potential infinity, wherein mathematics was only considered in the latter.[3] Carl Friedrich Gauss famously stated: "Infinity is nothing more than a figure of speech which helps us talk about limits. The notion of a completed infinity doesn't belong in mathematics."[4]
Development of mathematical set theory was motivated by several mathematicians. Bernhard Riemann's lecture On the Hypotheses which lie at the Foundations of Geometry (1854) proposed new ideas about topology, and about basing mathematics (especially geometry) in terms of sets or manifolds in the sense of a class (which he called Mannigfaltigkeit) now called point-set topology. The lecture was published by Richard Dedekind in 1868, along with Riemann's paper on trigonometric series (which presented the Riemann integral), The latter was a starting point a movement in real analysis for the study of “seriously” discontinuous functions. A young Georg Cantor entered into this area, which led him to the study of point-sets. Around 1871, influenced by Riemann, Dedekind began working with sets in his publications, which dealt very clearly and precisely with equivalence relations, partitions of sets, and homomorphisms. Thus, many of the usual set-theoretic procedures of twentieth-century mathematics go back to his work. However, he did not publish a formal explanation of his set theory until 1888.
Naive set theory
[edit]
Set theory, as understood by modern mathematicians, is generally considered to be founded by a single paper in 1874 by Georg Cantor titled On a Property of the Collection of All Real Algebraic Numbers.[5][6][7] In his paper, he developed the notion of cardinality, comparing the sizes of two sets by setting them in one-to-one correspondence. His "revolutionary discovery" was that the set of all real numbers is uncountable, that is, one cannot put all real numbers in a list. This theorem is proved using Cantor's first uncountability proof, which differs from the more familiar proof using his diagonal argument.
Cantor introduced fundamental constructions in set theory, such as the power set of a set A, which is the set of all possible subsets of A. He later proved that the size of the power set of A is strictly larger than the size of A, even when A is an infinite set; this result soon became known as Cantor's theorem. Cantor developed a theory of transfinite numbers, called cardinals and ordinals, which extended the arithmetic of the natural numbers. His notation for the cardinal numbers was the Hebrew letter (ℵ, aleph) with a natural number subscript; for the ordinals he employed the Greek letter (ω, omega).
Set theory was beginning to become an essential ingredient of the new “modern” approach to mathematics. Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections (see: Controversy over Cantor's theory).[a] Dedekind's algebraic style only began to find followers in the 1890s

Despite the controversy, Cantor's set theory gained remarkable ground around the turn of the 20th century with the work of several notable mathematicians and philosophers. Richard Dedekind, around the same time, began working with sets in his publications, and famously constructing the real numbers using Dedekind cuts. He also worked with Giuseppe Peano in developing the Peano axioms, which formalized natural-number arithmetic, using set-theoretic ideas, which also introduced the epsilon symbol for set membership. Possibly most prominently, Gottlob Frege began to develop his Foundations of Aritmetic.
In his work, Frege tries to ground all mathematics in terms of logical axioms using Cantor's cardinality. For example, the sentence "the number of horses in the barn is four" means that four objects fall under the concept horse in the barn. Frege attempted to explain our grasp of numbers through cardinality ('the number of...', or ), relying on Hume's principle.

However, Frege's work was short-lived, as it was found by Bertrand Russell that his axioms lead to a contradiction. Specifically, Frege's Basic Law V (now known as the axiom schema of unrestricted comprehension). According to Basic Law V, for any sufficiently well-defined property, there is the set of all and only the objects that have that property. The contradiction, called Russell's paradox, is shown as follows:
Let R be the set of all sets that are not members of themselves. (This set is sometimes called "the Russell set".) If R is not a member of itself, then its definition entails that it is a member of itself; yet, if it is a member of itself, then it is not a member of itself, since it is the set of all sets that are not members of themselves. The resulting contradiction is Russell's paradox. In symbols:
This came around a time of several paradoxes or counter-intuitive results. For example, that the parallel postulate cannot be proved, the existence of mathematical objects that cannot be computed or explicitly described, and the existence of theorems of arithmetic that cannot be proved with Peano arithmetic. The result was a foundational crisis of mathematics.
Basic concepts and notation
[edit]Set theory begins with a fundamental binary relation between an object o and a set A. If o is a member (or element) of A, the notation o ∈ A is used. A set is described by listing elements separated by commas, or by a characterizing property of its elements, within braces { }.[8] Since sets are objects, the membership relation can relate sets as well, i.e., sets themselves can be members of other sets.
A derived binary relation between two sets is the subset relation, also called set inclusion. If all the members of set A are also members of set B, then A is a subset of B, denoted A ⊆ B. For example, {1, 2} is a subset of {1, 2, 3}, and so is {2} but {1, 4} is not. As implied by this definition, a set is a subset of itself. For cases where this possibility is unsuitable or would make sense to be rejected, the term proper subset is defined. A is called a proper subset of B if and only if A is a subset of B, but A is not equal to B. Also, 1, 2, and 3 are members (elements) of the set {1, 2, 3}, but are not subsets of it; and in turn, the subsets, such as {1}, are not members of the set {1, 2, 3}. More complicated relations can exist; for example, the set {1} is both a member and a proper subset of the set {1, {1}}.
Just as arithmetic features binary operations on numbers, set theory features binary operations on sets.[9] The following is a partial list of them:
- Union of the sets A and B, denoted A ∪ B, is the set of all objects that are a member of A, or B, or both.[10] For example, the union of {1, 2, 3} and {2, 3, 4} is the set {1, 2, 3, 4}.
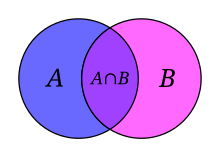
- Intersection of the sets A and B, denoted A ∩ B, is the set of all objects that are members of both A and B. For example, the intersection of {1, 2, 3} and {2, 3, 4} is the set {2, 3}.
- Set difference of U and A, denoted U \ A, is the set of all members of U that are not members of A. The set difference {1, 2, 3} \ {2, 3, 4} is {1}, while conversely, the set difference {2, 3, 4} \ {1, 2, 3} is {4}. When A is a subset of U, the set difference U \ A is also called the complement of A in U. In this case, if the choice of U is clear from the context, the notation Ac is sometimes used instead of U \ A, particularly if U is a universal set as in the study of Venn diagrams.
- Symmetric difference of sets A and B, denoted A △ B or A ⊖ B, is the set of all objects that are a member of exactly one of A and B (elements which are in one of the sets, but not in both). For instance, for the sets {1, 2, 3} and {2, 3, 4}, the symmetric difference set is {1, 4}. It is the set difference of the union and the intersection, (A ∪ B) \ (A ∩ B) or (A \ B) ∪ (B \ A).
- Cartesian product of A and B, denoted A × B, is the set whose members are all possible ordered pairs (a, b), where a is a member of A and b is a member of B. For example, the Cartesian product of {1, 2} and {red, white} is {(1, red), (1, white), (2, red), (2, white)}.
Some basic sets of central importance are the set of natural numbers, the set of real numbers and the empty set – the unique set containing no elements. The empty set is also occasionally called the null set,[11] though this name is ambiguous and can lead to several interpretations.
The power set of a set A, denoted , is the set whose members are all of the possible subsets of A. For example, the power set of {1, 2} is { {}, {1}, {2}, {1, 2} }. Notably, contains both A and the empty set.
Ontology
[edit]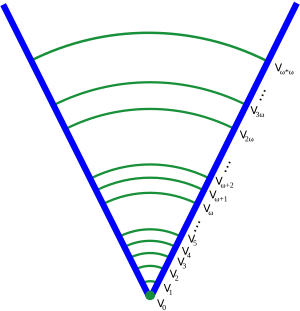
A set is pure if all of its members are sets, all members of its members are sets, and so on. For example, the set containing only the empty set is a nonempty pure set. In modern set theory, it is common to restrict attention to the von Neumann universe of pure sets, and many systems of axiomatic set theory are designed to axiomatize the pure sets only. There are many technical advantages to this restriction, and little generality is lost, because essentially all mathematical concepts can be modeled by pure sets. Sets in the von Neumann universe are organized into a cumulative hierarchy, based on how deeply their members, members of members, etc. are nested. Each set in this hierarchy is assigned (by transfinite recursion) an ordinal number , known as its rank. The rank of a pure set is defined to be the least ordinal that is strictly greater than the rank of any of its elements. For example, the empty set is assigned rank 0, while the set containing only the empty set is assigned rank 1. For each ordinal , the set is defined to consist of all pure sets with rank less than . The entire von Neumann universe is denoted .
Formalized set theory
[edit]Elementary set theory can be studied informally and intuitively, and so can be taught in primary schools using Venn diagrams. The intuitive approach tacitly assumes that a set may be formed from the class of all objects satisfying any particular defining condition. This assumption gives rise to paradoxes, the simplest and best known of which are Russell's paradox and the Burali-Forti paradox. Axiomatic set theory was originally devised to rid set theory of such paradoxes.[note 1]
The most widely studied systems of axiomatic set theory imply that all sets form a cumulative hierarchy.[b] Such systems come in two flavors, those whose ontology consists of:
- Sets alone. This includes the most common axiomatic set theory, Zermelo–Fraenkel set theory with the axiom of choice (ZFC). Fragments of ZFC include:
- Zermelo set theory, which replaces the axiom schema of replacement with that of separation;
- General set theory, a small fragment of Zermelo set theory sufficient for the Peano axioms and finite sets;
- Kripke–Platek set theory, which omits the axioms of infinity, powerset, and choice, and weakens the axiom schemata of separation and replacement.
- Sets and proper classes. These include Von Neumann–Bernays–Gödel set theory, which has the same strength as ZFC for theorems about sets alone, and Morse–Kelley set theory and Tarski–Grothendieck set theory, both of which are stronger than ZFC.
The above systems can be modified to allow urelements, objects that can be members of sets but that are not themselves sets and do not have any members.
The New Foundations systems of NFU (allowing urelements) and NF (lacking them), associate with Willard Van Orman Quine, are not based on a cumulative hierarchy. NF and NFU include a "set of everything", relative to which every set has a complement. In these systems urelements matter, because NF, but not NFU, produces sets for which the axiom of choice does not hold. Despite NF's ontology not reflecting the traditional cumulative hierarchy and violating well-foundedness, Thomas Forster has argued that it does reflect an iterative conception of set.[12]
Systems of constructive set theory, such as CST, CZF, and IZF, embed their set axioms in intuitionistic instead of classical logic. Yet other systems accept classical logic but feature a nonstandard membership relation. These include rough set theory and fuzzy set theory, in which the value of an atomic formula embodying the membership relation is not simply True or False. The Boolean-valued models of ZFC are a related subject.
An enrichment of ZFC called internal set theory was proposed by Edward Nelson in 1977.[13]
Applications
[edit]Many mathematical concepts can be defined precisely using only set theoretic concepts. For example, mathematical structures as diverse as graphs, manifolds, rings, vector spaces, and relational algebras can all be defined as sets satisfying various (axiomatic) properties. Equivalence and order relations are ubiquitous in mathematics, and the theory of mathematical relations can be described in set theory.[14][15]
Set theory is also a promising foundational system for much of mathematics. Since the publication of the first volume of Principia Mathematica, it has been claimed that most (or even all) mathematical theorems can be derived using an aptly designed set of axioms for set theory, augmented with many definitions, using first or second-order logic. For example, properties of the natural and real numbers can be derived within set theory, as each of these number systems can be defined by representing their elements as sets of specific forms.[16]
Set theory as a foundation for mathematical analysis, topology, abstract algebra, and discrete mathematics is likewise uncontroversial; mathematicians accept (in principle) that theorems in these areas can be derived from the relevant definitions and the axioms of set theory. However, it remains that few full derivations of complex mathematical theorems from set theory have been formally verified, since such formal derivations are often much longer than the natural language proofs mathematicians commonly present. One verification project, Metamath, includes human-written, computer-verified derivations of more than 12,000 theorems starting from ZFC set theory, first-order logic and propositional logic.[17]
Areas of study
[edit]Set theory is a major area of research in mathematics with many interrelated subfields:
Combinatorial set theory
[edit]Combinatorial set theory concerns extensions of finite combinatorics to infinite sets. This includes the study of cardinal arithmetic and the study of extensions of Ramsey's theorem such as the Erdős–Rado theorem.
Descriptive set theory
[edit]Descriptive set theory is the study of subsets of the real line and, more generally, subsets of Polish spaces. It begins with the study of pointclasses in the Borel hierarchy and extends to the study of more complex hierarchies such as the projective hierarchy and the Wadge hierarchy. Many properties of Borel sets can be established in ZFC, but proving these properties hold for more complicated sets requires additional axioms related to determinacy and large cardinals.
The field of effective descriptive set theory is between set theory and recursion theory. It includes the study of lightface pointclasses, and is closely related to hyperarithmetical theory. In many cases, results of classical descriptive set theory have effective versions; in some cases, new results are obtained by proving the effective version first and then extending ("relativizing") it to make it more broadly applicable.
A recent area of research concerns Borel equivalence relations and more complicated definable equivalence relations. This has important applications to the study of invariants in many fields of mathematics.
Fuzzy set theory
[edit]In set theory as Cantor defined and Zermelo and Fraenkel axiomatized, an object is either a member of a set or not. In fuzzy set theory this condition was relaxed by Lotfi A. Zadeh so an object has a degree of membership in a set, a number between 0 and 1. For example, the degree of membership of a person in the set of "tall people" is more flexible than a simple yes or no answer and can be a real number such as 0.75.
Inner model theory
[edit]An inner model of Zermelo–Fraenkel set theory (ZF) is a transitive class that includes all the ordinals and satisfies all the axioms of ZF. The canonical example is the constructible universe L developed by Gödel. One reason that the study of inner models is of interest is that it can be used to prove consistency results. For example, it can be shown that regardless of whether a model V of ZF satisfies the continuum hypothesis or the axiom of choice, the inner model L constructed inside the original model will satisfy both the generalized continuum hypothesis and the axiom of choice. Thus the assumption that ZF is consistent (has at least one model) implies that ZF together with these two principles is consistent.
The study of inner models is common in the study of determinacy and large cardinals, especially when considering axioms such as the axiom of determinacy that contradict the axiom of choice. Even if a fixed model of set theory satisfies the axiom of choice, it is possible for an inner model to fail to satisfy the axiom of choice. For example, the existence of sufficiently large cardinals implies that there is an inner model satisfying the axiom of determinacy (and thus not satisfying the axiom of choice).[18]
Large cardinals
[edit]A large cardinal is a cardinal number with an extra property. Many such properties are studied, including inaccessible cardinals, measurable cardinals, and many more. These properties typically imply the cardinal number must be very large, with the existence of a cardinal with the specified property unprovable in Zermelo–Fraenkel set theory.
Determinacy
[edit]Determinacy refers to the fact that, under appropriate assumptions, certain two-player games of perfect information are determined from the start in the sense that one player must have a winning strategy. The existence of these strategies has important consequences in descriptive set theory, as the assumption that a broader class of games is determined often implies that a broader class of sets will have a topological property. The axiom of determinacy (AD) is an important object of study; although incompatible with the axiom of choice, AD implies that all subsets of the real line are well behaved (in particular, measurable and with the perfect set property). AD can be used to prove that the Wadge degrees have an elegant structure.
Forcing
[edit]Paul Cohen invented the method of forcing while searching for a model of ZFC in which the continuum hypothesis fails, or a model of ZF in which the axiom of choice fails. Forcing adjoins to some given model of set theory additional sets in order to create a larger model with properties determined (i.e. "forced") by the construction and the original model. For example, Cohen's construction adjoins additional subsets of the natural numbers without changing any of the cardinal numbers of the original model. Forcing is also one of two methods for proving relative consistency by finitistic methods, the other method being Boolean-valued models.
Cardinal invariants
[edit]A cardinal invariant is a property of the real line measured by a cardinal number. For example, a well-studied invariant is the smallest cardinality of a collection of meagre sets of reals whose union is the entire real line. These are invariants in the sense that any two isomorphic models of set theory must give the same cardinal for each invariant. Many cardinal invariants have been studied, and the relationships between them are often complex and related to axioms of set theory.
Set-theoretic topology
[edit]Set-theoretic topology studies questions of general topology that are set-theoretic in nature or that require advanced methods of set theory for their solution. Many of these theorems are independent of ZFC, requiring stronger axioms for their proof. A famous problem is the normal Moore space question, a question in general topology that was the subject of intense research. The answer to the normal Moore space question was eventually proved to be independent of ZFC.
Controversy
[edit]From set theory's inception, some mathematicians have objected to it as a foundation for mathematics. The most common objection to set theory, one Kronecker voiced in set theory's earliest years, starts from the constructivist view that mathematics is loosely related to computation. If this view is granted, then the treatment of infinite sets, both in naive and in axiomatic set theory, introduces into mathematics methods and objects that are not computable even in principle. The feasibility of constructivism as a substitute foundation for mathematics was greatly increased by Errett Bishop's influential book Foundations of Constructive Analysis.[19]
A different objection put forth by Henri Poincaré is that defining sets using the axiom schemas of specification and replacement, as well as the axiom of power set, introduces impredicativity, a type of circularity, into the definitions of mathematical objects. The scope of predicatively founded mathematics, while less than that of the commonly accepted Zermelo–Fraenkel theory, is much greater than that of constructive mathematics, to the point that Solomon Feferman has said that "all of scientifically applicable analysis can be developed [using predicative methods]".[20]
Ludwig Wittgenstein condemned set theory philosophically for its connotations of mathematical platonism.[21] He wrote that "set theory is wrong", since it builds on the "nonsense" of fictitious symbolism, has "pernicious idioms", and that it is nonsensical to talk about "all numbers".[22] Wittgenstein identified mathematics with algorithmic human deduction;[23] the need for a secure foundation for mathematics seemed, to him, nonsensical.[24] Moreover, since human effort is necessarily finite, Wittgenstein's philosophy required an ontological commitment to radical constructivism and finitism. Meta-mathematical statements – which, for Wittgenstein, included any statement quantifying over infinite domains, and thus almost all modern set theory – are not mathematics.[25] Few modern philosophers have adopted Wittgenstein's views after a spectacular blunder in Remarks on the Foundations of Mathematics: Wittgenstein attempted to refute Gödel's incompleteness theorems after having only read the abstract. As reviewers Kreisel, Bernays, Dummett, and Goodstein all pointed out, many of his critiques did not apply to the paper in full. Only recently have philosophers such as Crispin Wright begun to rehabilitate Wittgenstein's arguments.[26]
Category theorists have proposed topos theory as an alternative to traditional axiomatic set theory. Topos theory can interpret various alternatives to that theory, such as constructivism, finite set theory, and computable set theory.[27][28] Topoi also give a natural setting for forcing and discussions of the independence of choice from ZF, as well as providing the framework for pointless topology and Stone spaces.[29]
An active area of research is the univalent foundations and related to it homotopy type theory. Within homotopy type theory, a set may be regarded as a homotopy 0-type, with universal properties of sets arising from the inductive and recursive properties of higher inductive types. Principles such as the axiom of choice and the law of the excluded middle can be formulated in a manner corresponding to the classical formulation in set theory or perhaps in a spectrum of distinct ways unique to type theory. Some of these principles may be proven to be a consequence of other principles. The variety of formulations of these axiomatic principles allows for a detailed analysis of the formulations required in order to derive various mathematical results.[30][31]
Mathematical education
[edit]As set theory gained popularity as a foundation for modern mathematics, there has been support for the idea of introducing the basics of naive set theory early in mathematics education.
In the US in the 1960s, the New Math experiment aimed to teach basic set theory, among other abstract concepts, to primary school students, but was met with much criticism. The math syllabus in European schools followed this trend, and currently includes the subject at different levels in all grades. Venn diagrams are widely employed to explain basic set-theoretic relationships to primary school students (even though John Venn originally devised them as part of a procedure to assess the validity of inferences in term logic).
Set theory is used to introduce students to logical operators (NOT, AND, OR), and semantic or rule description (technically intensional definition[32]) of sets (e.g. "months starting with the letter A"), which may be useful when learning computer programming, since Boolean logic is used in various programming languages. Likewise, sets and other collection-like objects, such as multisets and lists, are common datatypes in computer science and programming.
In addition to that, sets are commonly referred to in mathematical teaching when talking about different types of numbers (the sets of natural numbers, of integers, of real numbers, etc.), and when defining a mathematical function as a relation from one set (the domain) to another set (the range).
See also
[edit]- Glossary of set theory
- Class (set theory)
- List of set theory topics
- Relational model – borrows from set theory
- Venn diagram
- Elementary Theory of the Category of Sets
- Structural set theory
Notes
[edit]- ^ In his 1925 paper ""An Axiomatization of Set Theory", John von Neumann observed that "set theory in its first, "naive" version, due to Cantor, led to contradictions. These are the well-known antinomies of the set of all sets that do not contain themselves (Russell), of the set of all transfinite ordinal numbers (Burali-Forti), and the set of all finitely definable real numbers (Richard)." He goes on to observe that two "tendencies" were attempting to "rehabilitate" set theory. Of the first effort, exemplified by Bertrand Russell, Julius König, Hermann Weyl and L. E. J. Brouwer, von Neumann called the "overall effect of their activity . . . devastating". With regards to the axiomatic method employed by second group composed of Zermelo, Fraenkel and Schoenflies, von Neumann worried that "We see only that the known modes of inference leading to the antinomies fail, but who knows where there are not others?" and he set to the task, "in the spirit of the second group", to "produce, by means of a finite number of purely formal operations . . . all the sets that we want to see formed" but not allow for the antinomies. (All quotes from von Neumann 1925 reprinted in van Heijenoort, Jean (1967, third printing 1976), From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931, Harvard University Press, Cambridge MA, ISBN 0-674-32449-8 (pbk). A synopsis of the history, written by van Heijenoort, can be found in the comments that precede von Neumann's 1925 paper.
- ^ The objections to Cantor's work were occasionally fierce: Leopold Kronecker's public opposition and personal attacks included describing Cantor as a "scientific charlatan", a "renegade" and a "corrupter of youth". Kronecker objected to Cantor's proofs that the algebraic numbers are countable, and that the transcendental numbers are uncountable, results now included in a standard mathematics curriculum. Writing decades after Cantor's death, Wittgenstein lamented that mathematics is "ridden through and through with the pernicious idioms of set theory", which he dismissed as "utter nonsense" that is "laughable" and "wrong".
- ^ This is the converse for ZFC; V is a model of ZFC.
Citations
[edit]- ^ Ferreirós, José (2024), "The Early Development of Set Theory", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Winter 2024 ed.), Metaphysics Research Lab, Stanford University, retrieved 2025-01-04
- ^ Bolzano, Bernard (1975), Berg, Jan (ed.), Einleitung zur Größenlehre und erste Begriffe der allgemeinen Größenlehre, Bernard-Bolzano-Gesamtausgabe, edited by Eduard Winter et al., vol. II, A, 7, Stuttgart, Bad Cannstatt: Friedrich Frommann Verlag, p. 152, ISBN 3-7728-0466-7
- ^ Zenkin, Alexander (2004), "Logic Of Actual Infinity And G. Cantor's Diagonal Proof Of The Uncountability Of The Continuum", The Review of Modern Logic, vol. 9, no. 30, pp. 27–80
- ^ Dunham, William (1991), Journey through Genius: The Great Theorems of Mathematics, Penguin, p. 254, ISBN 9780140147391
- ^ Cantor, Georg (1874), "Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen", Journal für die reine und angewandte Mathematik (in German), 1874 (77): 258–262, doi:10.1515/crll.1874.77.258, S2CID 199545885
- ^ Johnson, Philip (1972), A History of Set Theory, Prindle, Weber & Schmidt, ISBN 0-87150-154-6
- ^ Dauben, Joseph (1979), Georg Cantor: His Mathematics and Philosophy of the Infinite, Harvard University Press, pp. 30–54, ISBN 0-674-34871-0.
- ^ "Introduction to Sets", www.mathsisfun.com, retrieved 2020-08-20
- ^ Kolmogorov, A.N.; Fomin, S.V. (1970), Introductory Real Analysis (Rev. English ed.), New York: Dover Publications, pp. 2–3, ISBN 0486612260, OCLC 1527264
- ^ "set theory | Basics, Examples, & Formulas", Encyclopedia Britannica, retrieved 2020-08-20
- ^ Bagaria, Joan (2020), "Set Theory", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2020 ed.), Metaphysics Research Lab, Stanford University, retrieved 2020-08-20
- ^ Forster, T. E. (2008), "The iterative conception of set" (PDF), The Review of Symbolic Logic, 1: 97–110, doi:10.1017/S1755020308080064, S2CID 15231169
- ^ Nelson, Edward (November 1977), "Internal Set Theory: a New Approach to Nonstandard Analysis", Bulletin of the American Mathematical Society, 83 (6): 1165, doi:10.1090/S0002-9904-1977-14398-X
- ^ "6.3: Equivalence Relations and Partitions", Mathematics LibreTexts, 2019-11-25, retrieved 2022-07-27
- ^ "Order Relations and Functions" (PDF), Web.stanford.edu, retrieved 2022-07-29
- ^ Mendelson, Elliott (1973), Number Systems and the Foundations of Analysis, Academic Press, MR 0357694, Zbl 0268.26001
- ^ "A PARTITION CALCULUS IN SET THEORY" (PDF), Ams.org, retrieved 2022-07-29
- ^ Jech, Thomas (2003), Set Theory, Springer Monographs in Mathematics (Third Millennium ed.), Berlin, New York: Springer-Verlag, p. 642, ISBN 978-3-540-44085-7, Zbl 1007.03002
- ^ Bishop, Errett (1967), Foundations of Constructive Analysis, New York: Academic Press, ISBN 4-87187-714-0
- ^ Feferman, Solomon (1998), In the Light of Logic, New York: Oxford University Press, pp. 280–283, 293–294, ISBN 0-195-08030-0
- ^ Rodych, Victor (Jan 31, 2018), "Wittgenstein's Philosophy of Mathematics", in Zalta, Edward N. (ed.), Stanford Encyclopedia of Philosophy (Spring 2018 ed.)
- ^ Wittgenstein, Ludwig (1975), Philosophical Remarks, §129, §174, Oxford: Basil Blackwell, ISBN 0-631-19130-5
- ^ Rodych 2018, §2.1: "When we prove a theorem or decide a proposition, we operate in a purely formal, syntactical manner. In doing mathematics, we do not discover pre-existing truths that were 'already there without one knowing' (PG 481)—we invent mathematics, bit-by-little-bit." Note, however, that Wittgenstein does not identify such deduction with philosophical logic; cf. Rodych §1, paras. 7-12.
- ^ Rodych 2018, §3.4: "Given that mathematics is a 'motley of techniques of proof' (RFM III, §46), it does not require a foundation (RFM VII, §16) and it cannot be given a self-evident foundation (PR §160; WVC 34 & 62; RFM IV, §3). Since set theory was invented to provide mathematics with a foundation, it is, minimally, unnecessary."
- ^ Rodych 2018, §2.2: "An expression quantifying over an infinite domain is never a meaningful proposition, not even when we have proved, for instance, that a particular number n has a particular property."
- ^ Rodych 2018, §3.6.
- ^ Ferro, Alfredo; Omodeo, Eugenio G.; Schwartz, Jacob T. (September 1980), "Decision Procedures for Elementary Sublanguages of Set Theory. I. Multi-Level Syllogistic and Some Extensions", Communications on Pure and Applied Mathematics, 33 (5): 599–608, doi:10.1002/cpa.3160330503
- ^ Cantone, Domenico; Ferro, Alfredo; Omodeo, Eugenio G. (1989), Computable Set Theory, International Series of Monographs on Computer Science, Oxford Science Publications, Oxford, UK: Clarendon Press, pp. xii, 347, ISBN 0-198-53807-3
- ^ Mac Lane, Saunders; Moerdijk, leke (1992), Sheaves in Geometry and Logic: A First Introduction to Topos Theory, Springer-Verlag, ISBN 978-0-387-97710-2
- ^ homotopy type theory at the nLab
- ^ Homotopy Type Theory: Univalent Foundations of Mathematics. The Univalent Foundations Program. Institute for Advanced Study.
- ^ Frank Ruda (6 October 2011), Hegel's Rabble: An Investigation into Hegel's Philosophy of Right, Bloomsbury Publishing, p. 151, ISBN 978-1-4411-7413-0
References
[edit]- Kunen, Kenneth (1980), Set Theory: An Introduction to Independence Proofs, North-Holland, ISBN 0-444-85401-0
- Johnson, Philip (1972), A History of Set Theory, Prindle, Weber & Schmidt, ISBN 0-87150-154-6
- Devlin, Keith (1993), The Joy of Sets: Fundamentals of Contemporary Set Theory, Undergraduate Texts in Mathematics (2nd ed.), Springer Verlag, doi:10.1007/978-1-4612-0903-4, ISBN 0-387-94094-4
- Ferreirós, Jose (2001), Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics, Berlin: Springer, ISBN 978-3-7643-5749-8
- Monk, J. Donald (1969), Introduction to Set Theory, McGraw-Hill Book Company, ISBN 978-0-898-74006-6
- Potter, Michael (2004), Set Theory and Its Philosophy: A Critical Introduction, Oxford University Press, ISBN 978-0-191-55643-2
- Smullyan, Raymond M.; Fitting, Melvin (2010), Set Theory and the Continuum Problem, Dover Publications, ISBN 978-0-486-47484-7
- Tiles, Mary (2004), The Philosophy of Set Theory: An Historical Introduction to Cantor's Paradise, Dover Publications, ISBN 978-0-486-43520-6
- Dauben, Joseph W. (1977), "Georg Cantor and Pope Leo XIII: Mathematics, Theology, and the Infinite", Journal of the History of Ideas, 38 (1): 85–108, doi:10.2307/2708842, JSTOR 2708842
- Dauben, Joseph W. (1979), [Unavailable on archive.org] Georg Cantor: his mathematics and philosophy of the infinite, Boston: Harvard University Press, ISBN 978-0-691-02447-9
External links
[edit]- Daniel Cunningham, Set Theory article in the Internet Encyclopedia of Philosophy.
- Jose Ferreiros, "The Early Development of Set Theory" article in the [Stanford Encyclopedia of Philosophy].
- Foreman, Matthew, Akihiro Kanamori, eds. Handbook of Set Theory. 3 vols., 2010. Each chapter surveys some aspect of contemporary research in set theory. Does not cover established elementary set theory, on which see Devlin (1993).
- "Axiomatic set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- "Set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Schoenflies, Arthur (1898). Mengenlehre in Klein's encyclopedia.
- Online books, and library resources in your library and in other libraries about set theory
- Rudin, Walter B. (April 6, 1990), "Set Theory: An Offspring of Analysis", Marden Lecture in Mathematics, University of Wisconsin-Milwaukee, archived from the original on 2021-10-31 – via YouTube
{{}}

![{\displaystyle [0,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/466c74a63ec8b8422ccb96c6bc5140dca45b5593)
![{\displaystyle [0,12]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89aabd85b3e389da4856956942ab5320c9bc586f)













